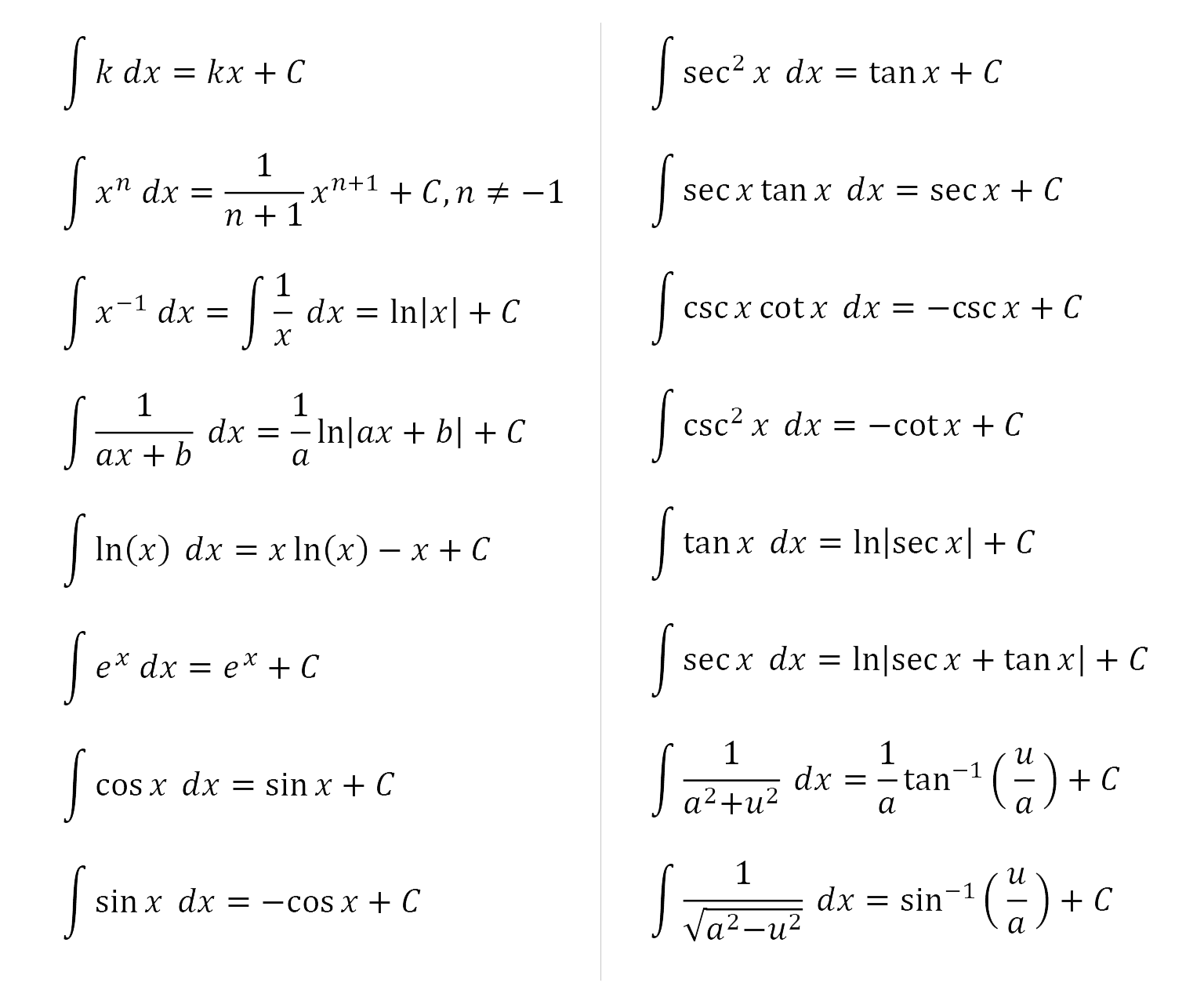Integration Rules Sheet

Integration Rules Sheet - If (𝑥=− (−𝑥), then ∫ (𝑥) 𝑥 − =0 undefined points: ∫ f ( x ) g ′ ( x ) dx = f ( x ) g ( x ) − ∫ g. (𝑥 ) 𝑥 =𝐹( )−𝐹( )=lim𝑥→ −𝐹𝑥− lim𝑥→ +𝐹(𝑥) )odd function: Integration can be used to find areas, volumes, central points and many useful things. The first rule to know is that. ∫ f ( g ( x )) g ′ ( x ) dx = ∫ f ( u ) du. If < < , and ( )is undefined, then ∫ (𝑥) 𝑥 =

(𝑥 ) 𝑥 =𝐹( )−𝐹( )=lim𝑥→ −𝐹𝑥− lim𝑥→ +𝐹(𝑥) )odd function: ∫ f ( x ) g ′ ( x ) dx = f ( x ) g ( x ) − ∫ g. The first rule to know is that. If (𝑥=− (−𝑥), then ∫ (𝑥) 𝑥 − =0 undefined points: ∫ f ( g ( x )) g ′ ( x ) dx = ∫ f ( u ) du. If < < , and ( )is undefined, then ∫ (𝑥) 𝑥 = Integration can be used to find areas, volumes, central points and many useful things.

Integration can be used to find areas, volumes, central points and many useful things. The first rule to know is that. ∫ f ( g ( x )) g ′ ( x ) dx = ∫ f ( u ) du. (𝑥 ) 𝑥 =𝐹( )−𝐹( )=lim𝑥→ −𝐹𝑥− lim𝑥→ +𝐹(𝑥) )odd function: If (𝑥=− (−𝑥), then ∫ (𝑥) 𝑥 − =0 undefined points: If < < , and ( )is undefined, then ∫ (𝑥) 𝑥 = ∫ f ( x ) g ′ ( x ) dx = f ( x ) g ( x ) − ∫ g.

Math for all integration farmula image

∫ f ( g ( x )) g ′ ( x ) dx = ∫ f ( u ) du. If < < , and ( )is undefined, then ∫ (𝑥) 𝑥 = If (𝑥=− (−𝑥), then ∫ (𝑥) 𝑥 − =0 undefined points: (𝑥 ) 𝑥 =𝐹( )−𝐹( )=lim𝑥→ −𝐹𝑥− lim𝑥→ +𝐹(𝑥) )odd function: The first rule to know.

Integration Rules, Properties, Formulas and Methods of Integration

(𝑥 ) 𝑥 =𝐹( )−𝐹( )=lim𝑥→ −𝐹𝑥− lim𝑥→ +𝐹(𝑥) )odd function: If < < , and ( )is undefined, then ∫ (𝑥) 𝑥 = If (𝑥=− (−𝑥), then ∫ (𝑥) 𝑥 − =0 undefined points: The first rule to know is that. ∫ f ( x ) g ′ ( x ) dx = f ( x ) g (.

Integration Rules Cheat Sheet

If (𝑥=− (−𝑥), then ∫ (𝑥) 𝑥 − =0 undefined points: ∫ f ( g ( x )) g ′ ( x ) dx = ∫ f ( u ) du. ∫ f ( x ) g ′ ( x ) dx = f ( x ) g ( x ) − ∫ g. If < < , and (.

Integration Rules and Formulas Math formula chart, Math formulas

Integration can be used to find areas, volumes, central points and many useful things. The first rule to know is that. (𝑥 ) 𝑥 =𝐹( )−𝐹( )=lim𝑥→ −𝐹𝑥− lim𝑥→ +𝐹(𝑥) )odd function: ∫ f ( x ) g ′ ( x ) dx = f ( x ) g ( x ) − ∫ g. If (𝑥=− (−𝑥), then ∫.

Integration Rules What are Integration Rules? Examples

Integration can be used to find areas, volumes, central points and many useful things. ∫ f ( x ) g ′ ( x ) dx = f ( x ) g ( x ) − ∫ g. The first rule to know is that. ∫ f ( g ( x )) g ′ ( x ) dx = ∫ f.

Integral cheat sheet Docsity

If < < , and ( )is undefined, then ∫ (𝑥) 𝑥 = Integration can be used to find areas, volumes, central points and many useful things. (𝑥 ) 𝑥 =𝐹( )−𝐹( )=lim𝑥→ −𝐹𝑥− lim𝑥→ +𝐹(𝑥) )odd function: If (𝑥=− (−𝑥), then ∫ (𝑥) 𝑥 − =0 undefined points: The first rule to know is that.

Integration Rules and Formulas A Plus Topper

Integration can be used to find areas, volumes, central points and many useful things. (𝑥 ) 𝑥 =𝐹( )−𝐹( )=lim𝑥→ −𝐹𝑥− lim𝑥→ +𝐹(𝑥) )odd function: ∫ f ( x ) g ′ ( x ) dx = f ( x ) g ( x ) − ∫ g. The first rule to know is that. ∫ f ( g (.

Integration Rules Integration table Math Original

If (𝑥=− (−𝑥), then ∫ (𝑥) 𝑥 − =0 undefined points: If < < , and ( )is undefined, then ∫ (𝑥) 𝑥 = (𝑥 ) 𝑥 =𝐹( )−𝐹( )=lim𝑥→ −𝐹𝑥− lim𝑥→ +𝐹(𝑥) )odd function: ∫ f ( x ) g ′ ( x ) dx = f ( x ) g ( x ) − ∫ g. ∫ f.

Integration Formulas Trig Definite Integrals Class My XXX Hot Girl

The first rule to know is that. If (𝑥=− (−𝑥), then ∫ (𝑥) 𝑥 − =0 undefined points: ∫ f ( x ) g ′ ( x ) dx = f ( x ) g ( x ) − ∫ g. Integration can be used to find areas, volumes, central points and many useful things. ∫ f ( g (.

Basic Integration Rules A Freshman's Guide to Integration

∫ f ( x ) g ′ ( x ) dx = f ( x ) g ( x ) − ∫ g. The first rule to know is that. If (𝑥=− (−𝑥), then ∫ (𝑥) 𝑥 − =0 undefined points: ∫ f ( g ( x )) g ′ ( x ) dx = ∫ f ( u ).

The First Rule To Know Is That.

If (𝑥=− (−𝑥), then ∫ (𝑥) 𝑥 − =0 undefined points: (𝑥 ) 𝑥 =𝐹( )−𝐹( )=lim𝑥→ −𝐹𝑥− lim𝑥→ +𝐹(𝑥) )odd function: Integration can be used to find areas, volumes, central points and many useful things. ∫ f ( x ) g ′ ( x ) dx = f ( x ) g ( x ) − ∫ g.