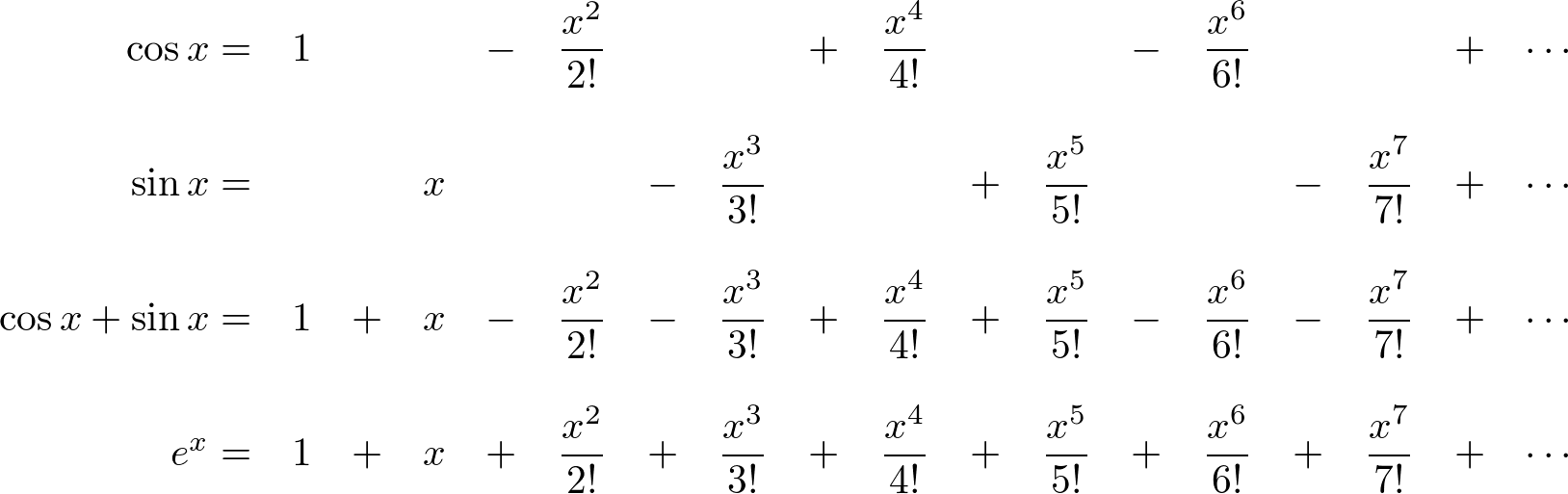Exponential Form Of Sin
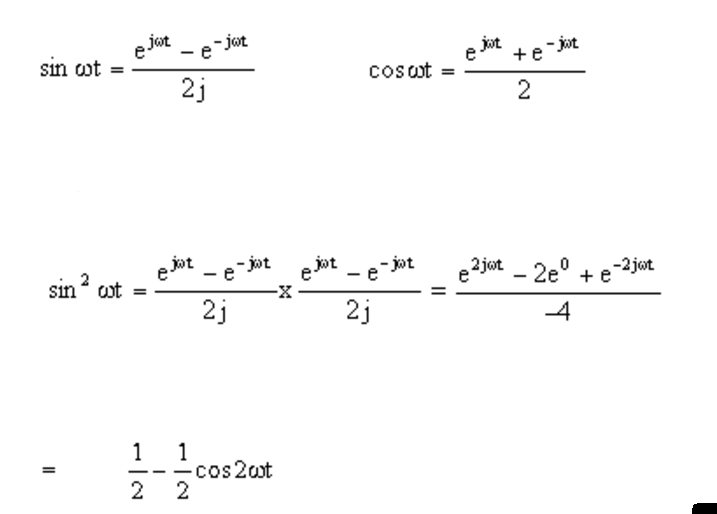
Exponential Form Of Sin - A field whose value varies as a sinusoidal function of time and of the distance from some. E^(ix) = sum_(n=0)^oo (ix)^n/(n!) =. Web an exponential equation is an equation that contains an exponential expression of the form b^x, where b is a constant (called the base) and x is a variable. Web well, sin z = 0 implies that eiz = e¡iz, so by multiplying both sides by eiz and using the addition formula for the complex exponential, we see that ei2z = 1, whereupon, by xi,. E^x = sum_(n=0)^oo x^n/(n!) so: Sinz = exp(iz) − exp( − iz) 2i. Web sinh x is half the difference of ex and e−x cosh x is the average of ex and e−x in terms of the exponential function: E jx = cos (x) + jsin (x) and the exponential representations of sin & cos, which are derived from euler's formula: The odd part of the exponential function,. Web #1 dough 19 0 hi, my question is from modern engineering mathematics by glyn james pg 177 # 17a using the exponential forms of cos (theta) and sin (theta).
E x = ∑ (k=0 to ∞) (x k / k!) = 1 + x + (x 2 / 2!) + (x 3 / 3!) +. Web according to euler, we should regard the complex exponential eit as related to the trigonometric functions cos(t) and sin(t) via the following inspired definition: E^x = sum_(n=0)^oo x^n/(n!) so: E jx = cos (x) + jsin (x) and the exponential representations of sin & cos, which are derived from euler's formula: A field whose value varies as a sinusoidal function of time and of the distance from some. Web an exponential equation is an equation that contains an exponential expression of the form b^x, where b is a constant (called the base) and x is a variable. Eit = cos t + i. Web the hyperbolic trigonometric functions extend the notion of the parametric equations for a unit circle \((x = \cos t\) and \(y = \sin t)\) to the parametric equations for a hyperbola,. Web well, sin z = 0 implies that eiz = e¡iz, so by multiplying both sides by eiz and using the addition formula for the complex exponential, we see that ei2z = 1, whereupon, by xi,. Web exponentials the exponential of a real number x, written e x or exp(x), is defined by an infinite series,.
What is going on, is that electrical engineers tend to ignore the fact that one needs to add or subtract the complex. Web well, sin z = 0 implies that eiz = e¡iz, so by multiplying both sides by eiz and using the addition formula for the complex exponential, we see that ei2z = 1, whereupon, by xi,. Sinz = exp(iz) − exp( − iz) 2i. Web the hyperbolic trigonometric functions extend the notion of the parametric equations for a unit circle \((x = \cos t\) and \(y = \sin t)\) to the parametric equations for a hyperbola,. Sinz denotes the complex sine function. Web relations between cosine, sine and exponential functions. E jx = cos (x) + jsin (x) and the exponential representations of sin & cos, which are derived from euler's formula: Web exponentials the exponential of a real number x, written e x or exp(x), is defined by an infinite series,. For any complex number z : Web #1 dough 19 0 hi, my question is from modern engineering mathematics by glyn james pg 177 # 17a using the exponential forms of cos (theta) and sin (theta).
Question Video Converting the Product of Complex Numbers in Polar Form
Web #1 dough 19 0 hi, my question is from modern engineering mathematics by glyn james pg 177 # 17a using the exponential forms of cos (theta) and sin (theta). Expz denotes the exponential function. A field whose value varies as a sinusoidal function of time and of the distance from some. E x = ∑ (k=0 to ∞) (x.
Basics of QPSK modulation and display of QPSK signals Electrical
For any complex number z : Sin z eiz e−iz = z −z3/3! Web #1 dough 19 0 hi, my question is from modern engineering mathematics by glyn james pg 177 # 17a using the exponential forms of cos (theta) and sin (theta). Web an exponential equation is an equation that contains an exponential expression of the form b^x, where.
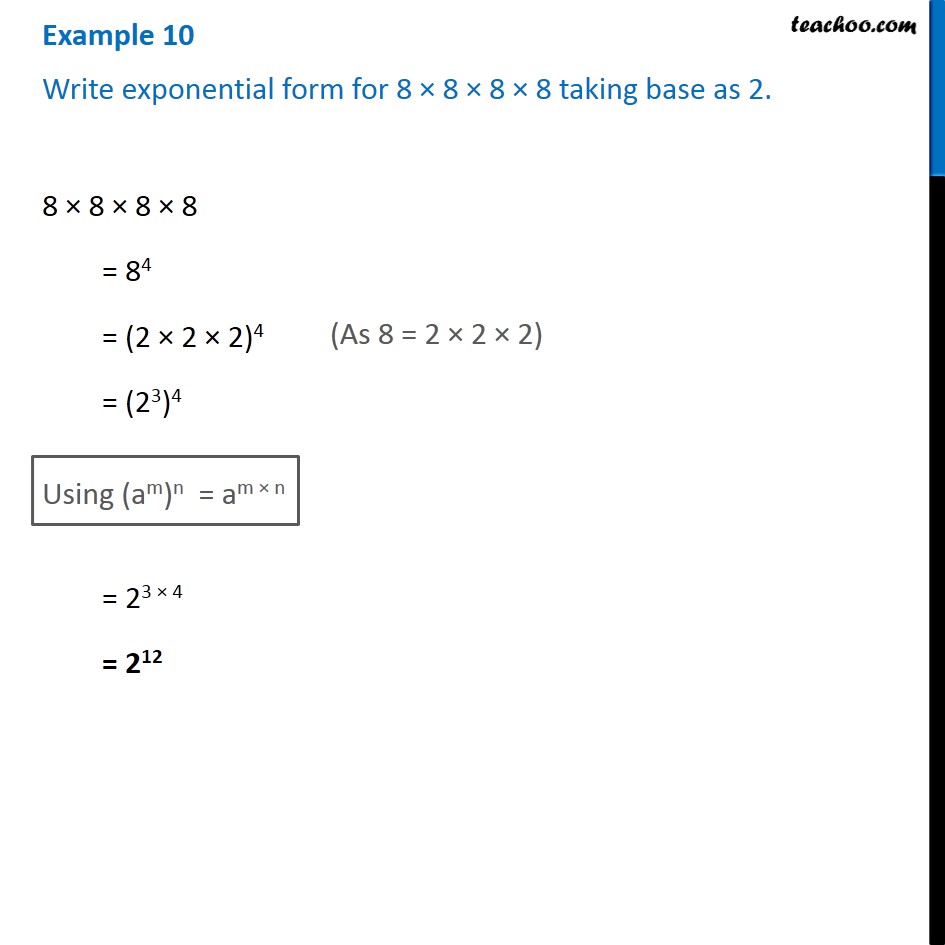
Example 10 Write exponential form for 8 x 8 x 8 x 8 taking base as 2
Web the hyperbolic trigonometric functions extend the notion of the parametric equations for a unit circle \((x = \cos t\) and \(y = \sin t)\) to the parametric equations for a hyperbola,. Prove eiz −e−iz = sin z e i z − e − i z = sin z. Web according to euler, we should regard the complex exponential eit.
Write Equations Of Sine Functions Using Properties Calculator
Web the hyperbolic trigonometric functions extend the notion of the parametric equations for a unit circle \((x = \cos t\) and \(y = \sin t)\) to the parametric equations for a hyperbola,. Sin z eiz e−iz = z −z3/3! Prove eiz −e−iz = sin z e i z − e − i z = sin z. Web an exponential equation.
Euler's Equation
Prove eiz −e−iz = sin z e i z − e − i z = sin z. Sin z eiz e−iz = z −z3/3! Web relations between cosine, sine and exponential functions. (45) (46) (47) from these relations and the properties of exponential multiplication you can painlessly prove all. Web according to euler, we should regard the complex exponential eit.
Other Math Archive January 29, 2018
Web #1 dough 19 0 hi, my question is from modern engineering mathematics by glyn james pg 177 # 17a using the exponential forms of cos (theta) and sin (theta). E jx = cos (x) + jsin (x) and the exponential representations of sin & cos, which are derived from euler's formula: Web expressing the sine function in terms of.
Exponents lesson 4 numbers in exponential form raised to a power
Web the hyperbolic trigonometric functions extend the notion of the parametric equations for a unit circle \((x = \cos t\) and \(y = \sin t)\) to the parametric equations for a hyperbola,. Web an exponential equation is an equation that contains an exponential expression of the form b^x, where b is a constant (called the base) and x is a.
How to find the exponential form of a number
Web relations between cosine, sine and exponential functions. Web sinh x is half the difference of ex and e−x cosh x is the average of ex and e−x in terms of the exponential function: E jx = cos (x) + jsin (x) and the exponential representations of sin & cos, which are derived from euler's formula: Eit = cos t.
Particular solution for sin using complex exponentials YouTube
Web expressing the sine function in terms of exponential. Sinz = exp(iz) − exp( − iz) 2i. Web well, sin z = 0 implies that eiz = e¡iz, so by multiplying both sides by eiz and using the addition formula for the complex exponential, we see that ei2z = 1, whereupon, by xi,. Web exponentials the exponential of a real.
Imaginary Number Calculator Wolfram IMAGECROT
Sinz denotes the complex sine function. Expz denotes the exponential function. E^x = sum_(n=0)^oo x^n/(n!) so: Web #1 dough 19 0 hi, my question is from modern engineering mathematics by glyn james pg 177 # 17a using the exponential forms of cos (theta) and sin (theta). A field whose value varies as a sinusoidal function of time and of the.
Web Expressing The Sine Function In Terms Of Exponential.
(45) (46) (47) from these relations and the properties of exponential multiplication you can painlessly prove all. Web #1 dough 19 0 hi, my question is from modern engineering mathematics by glyn james pg 177 # 17a using the exponential forms of cos (theta) and sin (theta). What is going on, is that electrical engineers tend to ignore the fact that one needs to add or subtract the complex. Eit = cos t + i.
Sinz = Exp(Iz) − Exp( − Iz) 2I.
E^x = sum_(n=0)^oo x^n/(n!) so: Web according to euler, we should regard the complex exponential eit as related to the trigonometric functions cos(t) and sin(t) via the following inspired definition: Sin z eiz e−iz = z −z3/3! The odd part of the exponential function,.
For Any Complex Number Z :
Web the hyperbolic trigonometric functions extend the notion of the parametric equations for a unit circle \((x = \cos t\) and \(y = \sin t)\) to the parametric equations for a hyperbola,. Sinz denotes the complex sine function. E^(ix) = sum_(n=0)^oo (ix)^n/(n!) =. Web an exponential equation is an equation that contains an exponential expression of the form b^x, where b is a constant (called the base) and x is a variable.
Expz Denotes The Exponential Function.
Web in physics, a sinusoidal (or monochromatic) plane wave is a special case of plane wave: A field whose value varies as a sinusoidal function of time and of the distance from some. Prove eiz −e−iz = sin z e i z − e − i z = sin z. E x = ∑ (k=0 to ∞) (x k / k!) = 1 + x + (x 2 / 2!) + (x 3 / 3!) +.